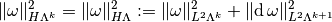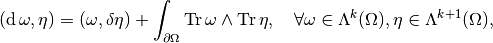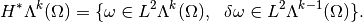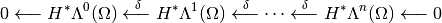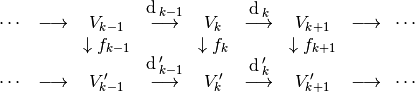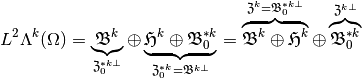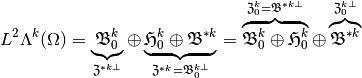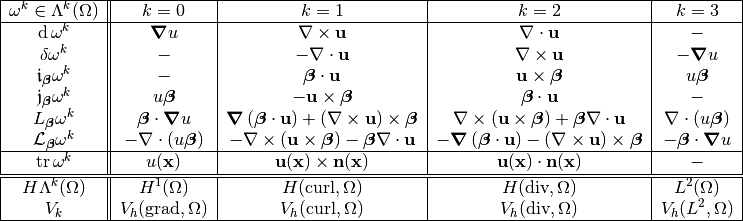Exterior Algebra¶
Let 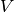 be a real vector space of dimension
be a real vector space of dimension 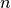 .
.
Definition, Alternating algebraic forms:
For each  , we define
, we define 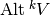 as the space of alternating
as the space of alternating  -linear maps
-linear maps  .
.
Note
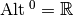 ,
,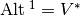 is the dual space of
is the dual space of 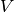 (the space of covectors)
(the space of covectors)
Definition, Exterior product:
For 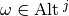 and
and 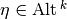 , their exterior (wedge) product is given by:
, their exterior (wedge) product is given by:
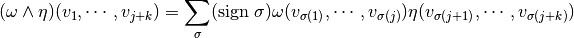
for all 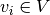 . Where the sum is over all permutations
. Where the sum is over all permutations 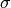 of
of 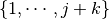 ,
for which
,
for which 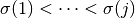 and
and 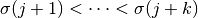 .
.
Note
- The exterior product is bilinear, associative,
- anti-commutative:
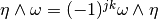 for all
for all 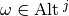 and
and 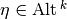 .
.
Definition, Grassmann Algebra:
Grassmann Algebra is defined by:
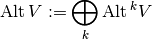
This is a anti-commutative graded algebra. Also called Exterior Algebra of 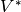
In the case of 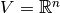 , we have:
, we have:
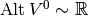 ,
,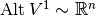 ,
,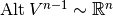 , using Riesz representation theorem,
, using Riesz representation theorem,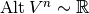 , using the map
, using the map 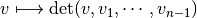 .
.
Basis¶
Let 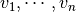 be a basis of
be a basis of 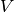 and
and 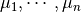 the associated dual basis for
the associated dual basis for 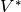 (
(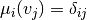 ).
).
For any increasing permutations 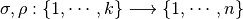 , we have:
, we have:
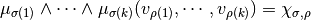
thus the 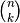 algebraic
algebraic  -forms
-forms 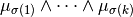 ,
form a basis for
,
form a basis for 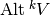 and
and 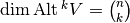 .
.
Definition, Interior product:
Let 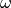 be a
be a  -form, and
-form, and 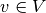 . The interior product of
. The interior product of 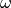 and
and  is the
is the 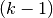 -form
-form 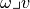 defined by:
defined by:
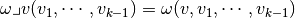
- We have for
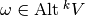 ,
, 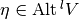 and
and 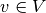 :
:
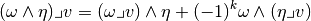
Definition, Inner product:
If 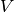 is has an inner product, then
is has an inner product, then 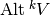 is endowed with an inner product given by:
is endowed with an inner product given by:
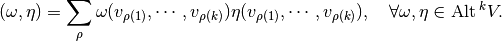
where the sum is over increasing sequences  , and
, and  is any orthonormal basis.
is any orthonormal basis.
Orientation and Volume form¶
Todo
add Orientation and Volume form
Definition, Pullback:
A linear transformation of vector spaces 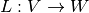 induces a transformation
induces a transformation
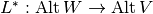 , called the pullback, and given by:
, called the pullback, and given by:
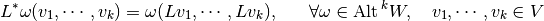
The pullback acts contravariantly: if
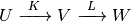 then,
then,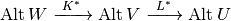
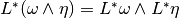
Let V be a subspace of W. For the inclusion 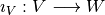 , we can define its pullback
, we can define its pullback 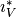 :
this is a surjection of
:
this is a surjection of 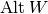 onto
onto 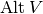 .
.
If W has an inner product and 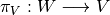 is the orthogonal projection. We can define its pullback
is the orthogonal projection. We can define its pullback 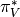 :
this an injection of
:
this an injection of 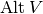 onto
onto 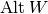 .
.
Let us consider the composition : 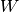 shortstack{
shortstack{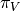 \
\  }
} 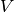 shortstack{
shortstack{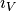 \
\  }
} 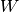 , and its pullback
, and its pullback 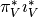 .
.
Definition, The tangential and normal parts:
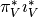 associates for each
associates for each 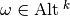 its tangential part
its tangential part  with respect to
with respect to  :
:
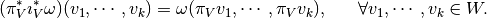
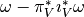 associates for each
associates for each 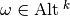 its normal part
its normal part 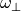 with respect to
with respect to 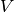 .
.
The tangential part of 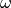 vanishes if and only if the image of
vanishes if and only if the image of 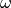 in
in 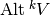 vanishes.
vanishes.
Let 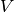 be an oriented inner product space, with volume form
be an oriented inner product space, with volume form 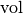 . Let
. Let 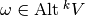 .
We can define a new linear map
.
We can define a new linear map 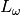 as the composition of
as the composition of 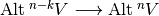 such as:
such as:
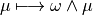
and the canonical isomorphism of 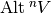 onto
onto 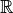 , and using the Riesz representation theorem,
there exists an element
, and using the Riesz representation theorem,
there exists an element 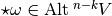 such that :
such that : 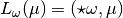 , i.e.:
, i.e.:
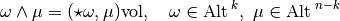
Definition, The Hodge star operation:
The linear map which maps 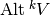 onto
onto 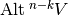
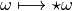 is called the Hodge star operator.
is called the Hodge star operator.
- If
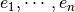 is any positively oriented orthonormal basis, and
is any positively oriented orthonormal basis, and 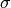 a permutation, we have
a permutation, we have
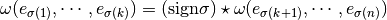
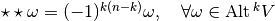 , thus the Hodge star is an isometry.
, thus the Hodge star is an isometry.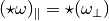 and
and 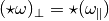
- the image of
 in
in 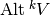 vanishes if and only if
vanishes if and only if  vanishes.
vanishes.
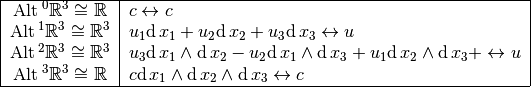
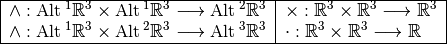
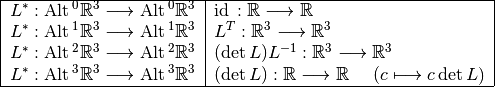


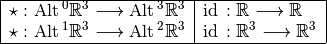
Exterior Calculus on manifolds and Differential forms¶
Let 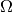 be a smooth manifold, of dimension
be a smooth manifold, of dimension 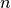 .
.
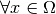 we denote by
we denote by 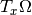 the tangent space. This is a vector space of dimension
the tangent space. This is a vector space of dimension 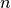 ,
,- tangent bundle
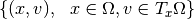 ,
, - Applying the exterior algebra to the tangent spaces, we obtain the exterior forms bundle, whose elements are pairs
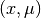 with
with 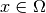 and
and 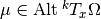 .
. - a differential
 -form
-form 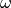 is a section of this bundle. This is a map which associates to each
is a section of this bundle. This is a map which associates to each 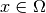 an element
an element 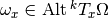 ,
, - if the map
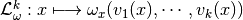 is smooth (whenever
is smooth (whenever 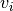 are smooth), we say that
are smooth), we say that 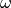 is a smooth differential
is a smooth differential  -form,
-form, - we define
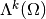 the space of all smooth
the space of all smooth  -forms on
-forms on 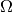 ,
, 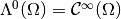 ,
,- if the map
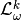 is
is 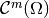 , we define differential
, we define differential  -forms with less smoothness
-forms with less smoothness 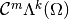 .
.
Let 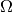 be a smooth manifold, of dimension
be a smooth manifold, of dimension 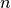 .
.
Exterior product:
if 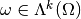 and
and 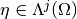 , we may define
, we may define 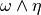 as
as 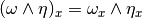 and the Grassmann algebra
and the Grassmann algebra 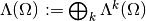
Differential forms can be differentiated and integrated, without recourse to any additional structure, such as a metric or a measure.
Exterior differentiation:
For each, can define the
-form
, such as:
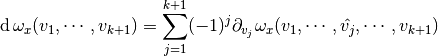
where the hat is used to indicated a suppressed argument.
This defines a graded linear operator of degree 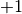 , of
, of 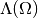 onto
onto 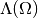 .
.
We have the following properties:
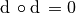
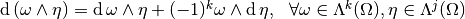 ,
,- (Pullback) let
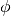 be a smooth map of
be a smooth map of 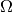 onto
onto 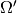 . Then
. Then 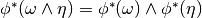 and
and 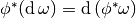 ,
, - (Interior product) the interior product of a differential
 -form
-form 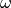 with a vector field
with a vector field  ,
, - we obtain a
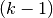 -form by :
-form by : 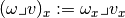 ,
, - (Trace operator) the pullback
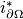 of
of 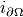 is the trace operator
is the trace operator 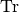
Integration:
- If
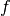 is an oriented, piecewise smooth
is an oriented, piecewise smooth  -dimensional submanifold of
-dimensional submanifold of 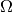 , and
, and 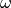 is a continuous
is a continuous  -form, then th integral
-form, then th integral 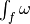 is well defined :
is well defined :- [0-forms] can be evaluated at points,
- [1-forms] can be integrated over directed curves,
- [2-forms] can be integrated over directed surfaces,
- (Inner product) The
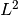 -inner product of two differential
-inner product of two differential  -forms on an oriented Riemannian manifold
-forms on an oriented Riemannian manifold 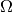 is defined as :
is defined as :
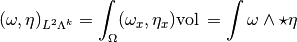
The completion of 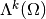 in the corresponding norm defines the Hilbert space
in the corresponding norm defines the Hilbert space 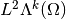 .
.
We have the following results:
- (Integration) if
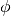 is an orientation-preserving diffeomorphism, then
is an orientation-preserving diffeomorphism, then
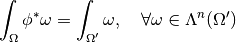
Theorem, Stokes theorem:
If 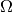 is an oriented
is an oriented 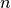 -manifold with boundary
-manifold with boundary 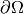 , then
, then
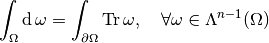
Theorem, Integration by parts:
If 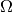 is an oriented
is an oriented 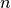 -manifold with boundary
-manifold with boundary 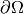 , then
, then
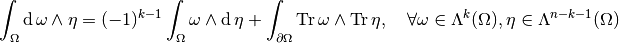
Sobolev spaces of differential forms¶
As for the classical case, we can define the Sobolev spaces as:
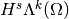 is the space of differential
is the space of differential  -forms such that
-forms such that 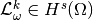 .
.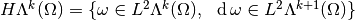 . The associated norm is :
. The associated norm is :
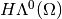 coincides with
coincides with 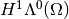 ,
,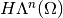 coincides with
coincides with 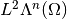 ,
,- for
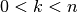 , we have
, we have 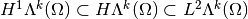 , strictly.
, strictly.
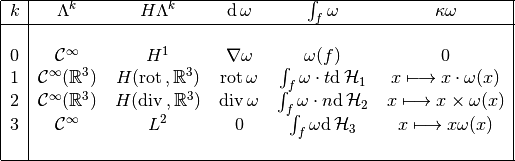
Cohomology and De Rham Complex¶
The De Rham complex is the sequence of spaces and mappings
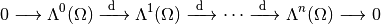
Since, 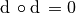 , we have
, we have
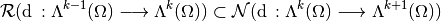
If 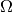 is an oriented Riemannian manifold, we have the following cohomology:
is an oriented Riemannian manifold, we have the following cohomology:
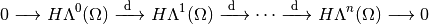
The coderivative operator 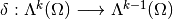 is defined as:
is defined as:
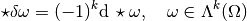
- we have
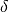 is a graded linear operator of degree
is a graded linear operator of degree 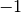 .
.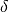 is the formal adjoint of
is the formal adjoint of 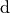 whenever
whenever 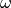 or
or 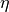 vanishes near the boundary.
vanishes near the boundary.- we define the spaces
we have
.
- we obtain the dual complex
Cohomology with boundary conditions¶
Let 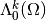 be the subspace of
be the subspace of 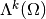 of smooth
of smooth  -forms with compact support. We have
-forms with compact support. We have 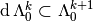 .
.
The De Rham complex with the compact support is
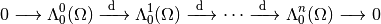
Recall that the closure of 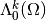 in
in 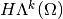 is
is
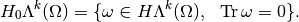
The 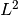 version of the last complex is
version of the last complex is
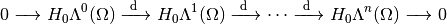
Definition, Harmonic forms:
The harmonic  -forms are the differential
-forms are the differential  -forms that verify the differential equations
-forms that verify the differential equations
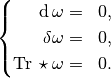
this defines the following space,
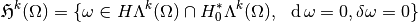
We can also define the following space,
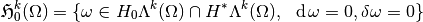
As we can see, 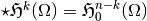 .
.
Proposition, Poincaré duality:
There is an isomorphism between the  th De Rham cohomology space and the
th De Rham cohomology space and the 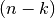 th cohomology space with boundary conditions.
th cohomology space with boundary conditions.
Homological Algebra and Hilbert complexes¶
Homological Algebra¶
- A cochain complex is a sequence of vector spaces and linear maps
 -cocycles
-cocycles 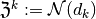 ,
, -coboundaries
-coboundaries 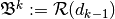 ,
, -cohomology
-cohomology 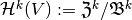 ,
,- we say that the sequence is exact, if the cohomology vanishes (i.e.
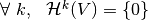 ),
), - Given two cochain complexes
 , a cochain map
, a cochain map 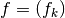 (such as
(such as 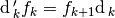 )
)
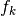 maps
maps  -cochains to
-cochains to  -cochains and
-cochains and  -coboundaries to
-coboundaries to  -coboundaries, thus induces a map
-coboundaries, thus induces a map 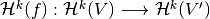 .
.
Let 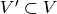 be two cochain complexes,
be two cochain complexes,
The inclusion
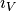 is a cochain map and thus induces a map of cohomology
is a cochain map and thus induces a map of cohomology 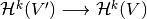 ,
,If there exists a cochain projection of
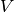 onto
onto 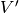 , (this leads to
, (this leads to 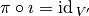 ) so
) so 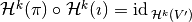 .
.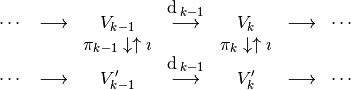
Thus, 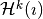 is injective and
is injective and 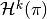 is surjective. Hence, if one of the cohomology spaces
is surjective. Hence, if one of the cohomology spaces 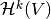 vanishes,
then so does
vanishes,
then so does 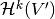
Cycles and boundaries of the De Rham complex¶
 -cocycles
-cocycles
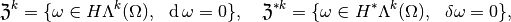
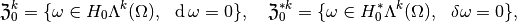
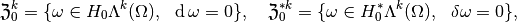
 -coboundaries
-coboundaries
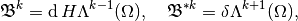
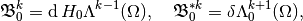
- each of the spaces of cycles is closed in
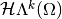 (
(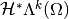 ), as well in
), as well in 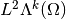 .
. - each of the spaces of boundaries is closed in
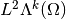 .
. - let
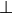 denotes the orthogonal complement in
denotes the orthogonal complement in 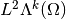 ,
,