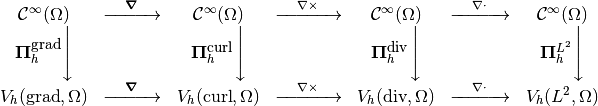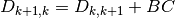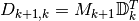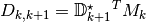DeRham sequences¶
here without boundary conditions
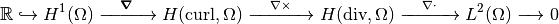
Pullbacks¶
In the case where the physical domain 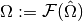 is the image of a logical domain
is the image of a logical domain 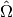 by a smooth mapping
by a smooth mapping 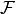 (at least
(at least 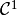 ), we have the following parallel diagrams
), we have the following parallel diagrams
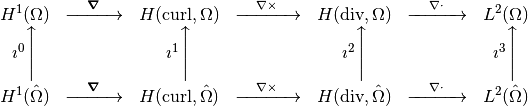
Where the mappings  and
and  are called pullbacks and are given by
are called pullbacks and are given by
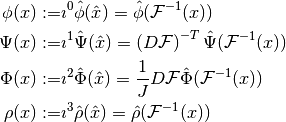
where 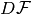 is the jacobian matrix of the mapping
is the jacobian matrix of the mapping 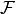 .
.
Note
The pullbacks 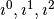 and
and 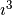 are isomorphisms between the corresponding spaces.
are isomorphisms between the corresponding spaces.
Discrete Spaces¶
Let us suppose that we have a sequence of finite subspaces for each of the spaces involved in the DeRham sequence. The discrete DeRham sequence stands for the following commutative diagram between continuous and discrete spaces
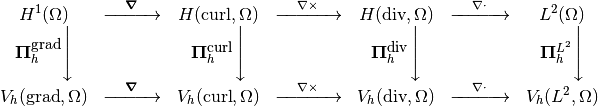
When using a Finite Elements methods, we often deal with a reference element, and thus we need also to apply the pullbacks on the discrete spaces. In fact, we have again the following parallel diagram
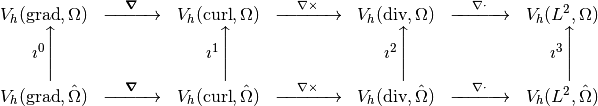
Since, the pullbacks are isomorphisms in the previous diagram, we can define a one-to-one correspondance
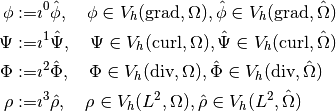
We have then, the following results
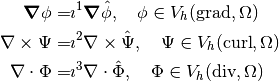
Discrete DeRham sequence for B-Splines¶
Buffa et al [BSV09] show the construction of a discrete DeRham sequence using B-Splines, (here without boundary conditions)
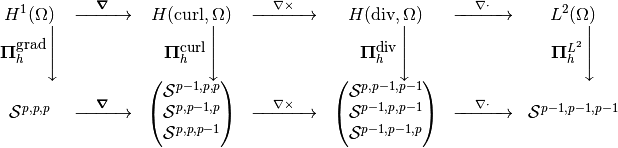
1d case¶
- DeRham sequence is reduced to
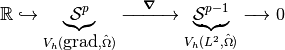
- The recursion formula for derivative writes

- we have
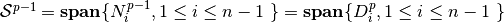 which is a change of basis as a diagonal matrix
which is a change of basis as a diagonal matrix - Now if
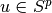 , with and expansion
, with and expansion 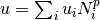 , we have
, we have
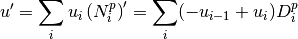
- If we introduce the B-Splines coefficients vector
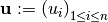 (and
(and 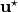 for the derivative), we have
for the derivative), we have
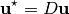
where 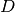 is the incidence matrix (of entries
is the incidence matrix (of entries 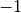 and
and 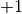 )
)
Discrete derivatives:
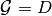
2d case¶
In 2d, the are two De-Rham complexes:
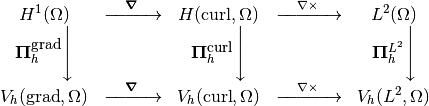
and
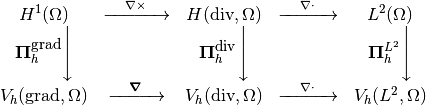
Let 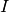 be the identity matrix, we have
be the identity matrix, we have
Discrete derivatives:
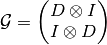
![\mathcal{C} =
\begin{pmatrix}
I \otimes D
\\
- D \otimes I
\end{pmatrix}
\quad \mbox{[scalar curl],} \quad
\mathcal{C} =
\begin{pmatrix}
- I \otimes D
&
D \otimes I
\end{pmatrix}
\quad \mbox{[vectorial curl]}](../_images/math/409e0105fb79c34ef7fc89a070283d24afc00575.png)
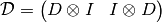
3d case¶
Discrete derivatives:
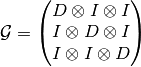
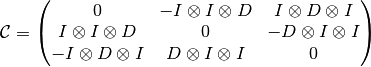
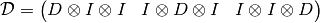
Note
From now on, we will denote the discrete derivative by 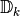 for the one going from
for the one going from 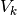 to
to 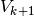 .
.
Algebraic identities¶
Let us consider the discretization of the exterior derivative
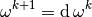
multiplying by a test function 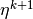 and integrating over the whole computation domain, we get
and integrating over the whole computation domain, we get
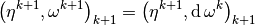
let 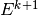 ,
, 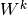 and
and 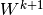 be the vector representation of
be the vector representation of 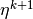 ,
, 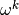 and
and 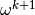 . We get
. We get
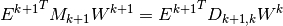
where
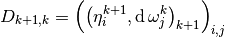
On the other hand, using the coderivative, we get
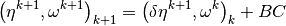
Let us now introduce the following matrix
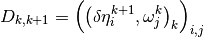
hence,
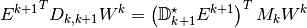
Therefor, we have the following important result
Proposition:
References
| [BSV09] | A. Buffa, G. Sangalli, and R. Vazquez. Isogeometric analysis in electromagnetics: b-splines approximation. Comput. Methods Appl. Mech. Engrg, 199:1143–1152, 2009. |