B-Splines and NURBS¶
We start this section by recalling some basic properies about B-splines curves and surfaces. We also recall some fundamental algorithms (knot insertion and degree elevation).
For a basic introduction to the subject, we refer to the books [LP95] and [Far02].
A B-Splines family, 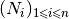 of order
of order 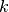 , can be generated using a non-decreasing sequence of knots
, can be generated using a non-decreasing sequence of knots 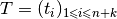 .
.
B-Splines series¶
The j-th B-Spline of order 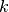 is defined by the recurrence relation:
is defined by the recurrence relation:
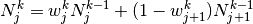
where,

for 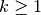 and
and 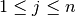 .
.
We note some important properties of a B-splines basis:
- B-splines are piecewise polynomial of degree
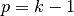 ,
, - Compact support; the support of
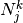 is contained in
is contained in ![\left[ t_j, t_{j+k} \right]](../_images/math/123ad99deea307dd580b2eca671cf82407cd64a4.png) ,
, - If
![x \in~ ] t_j,t_{j+1} [](../_images/math/3e1d714facac1f93fbb78d5073622c19a234be42.png) , then only the B-splines
, then only the B-splines 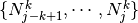 are non vanishing at
are non vanishing at 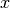 ,
, - Positivity:
![\forall j \in \{1,\cdots,n \}~~N_j(x) >0, ~~\forall x \in ] t_j, t_{j+k} [](../_images/math/e247cddc2012ac7fc0a6c66de300533eb5e27dc3.png) ,
, - Partition of unity
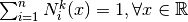 ,
, - Local linear independence,
- If a knot
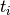 has a multiplicity
has a multiplicity 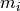 then the B-spline is
then the B-spline is 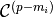 at
at 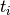 .
.
Knots vector families¶
There are two kind of knots vectors, called clamped and unclamped. Both families contains uniform and non-uniform sequences.
The following are examples of such knots vectors
- Clamped knots (open knots vector)
- uniform
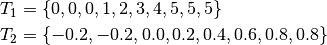
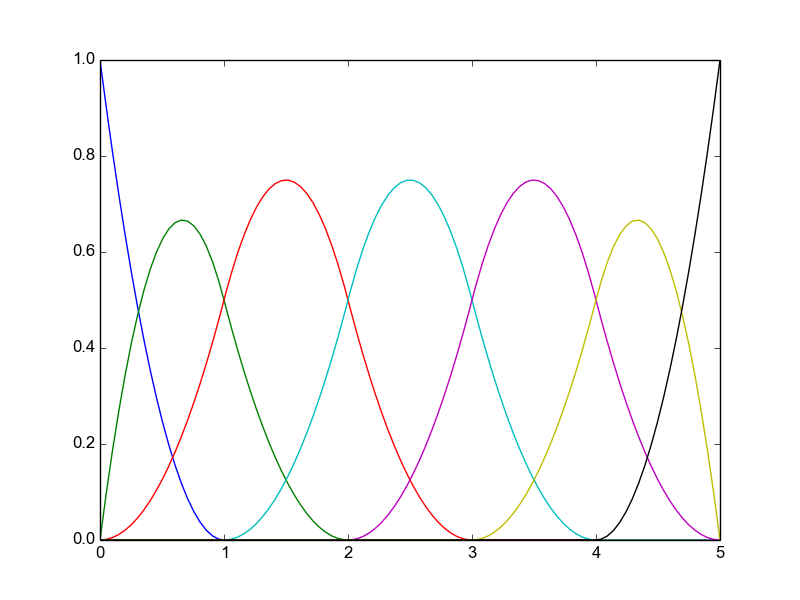
- non-uniform
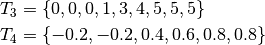
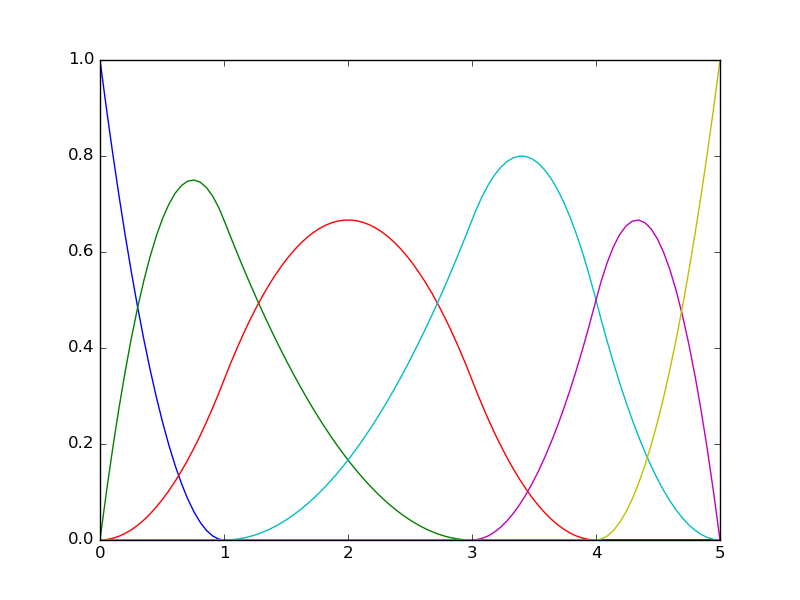
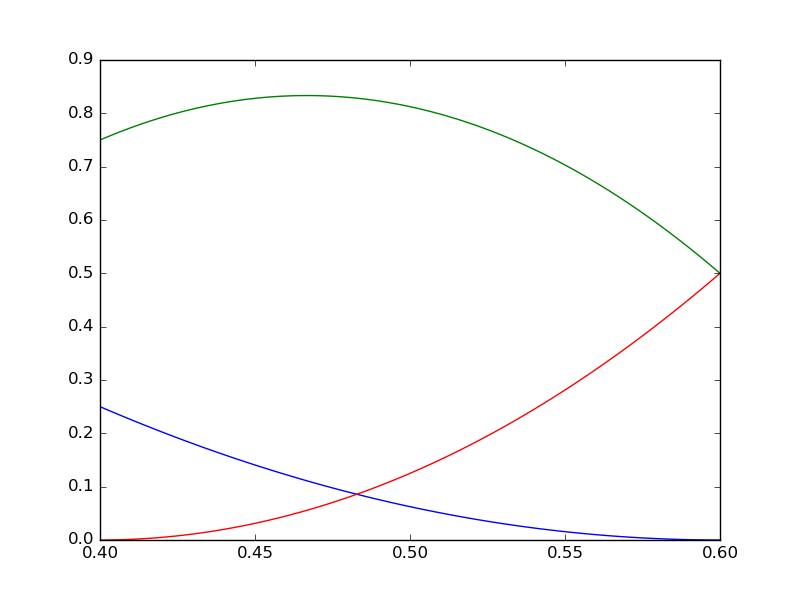
- Unclamped knots
- uniform
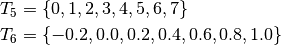
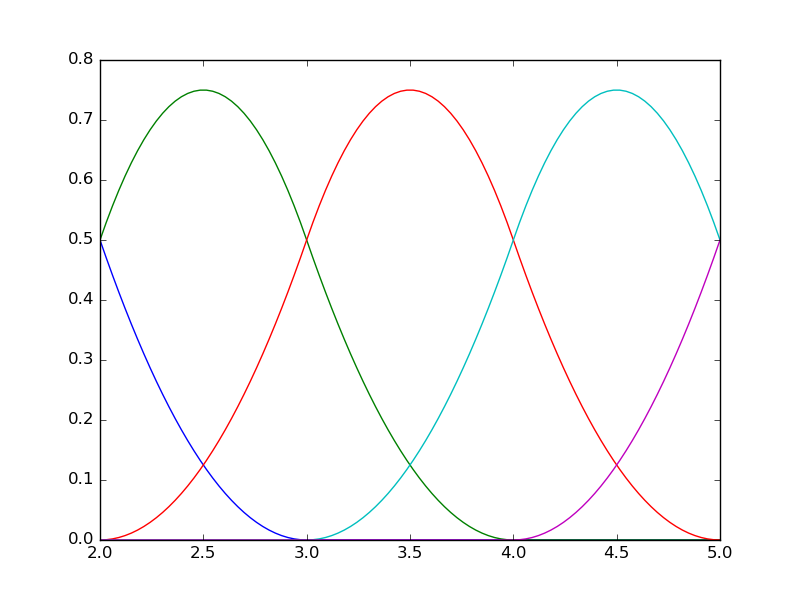
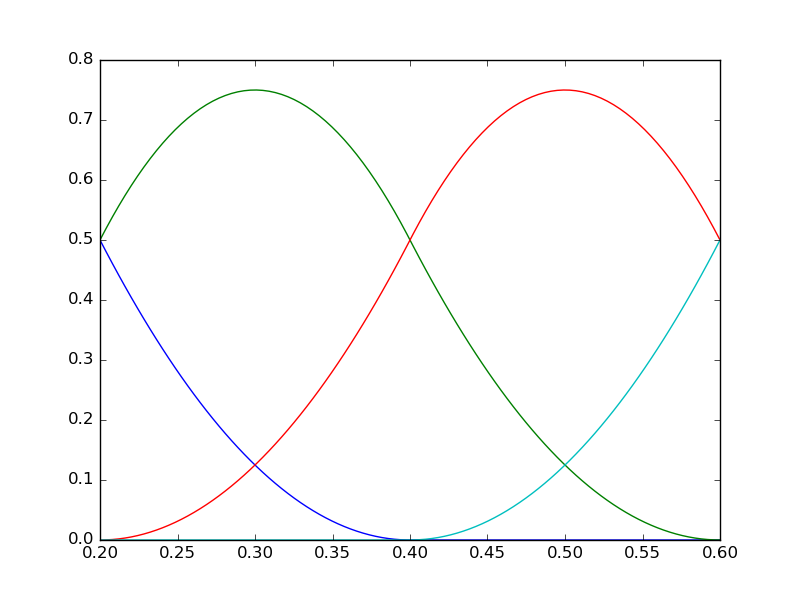
- non-uniform
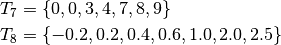
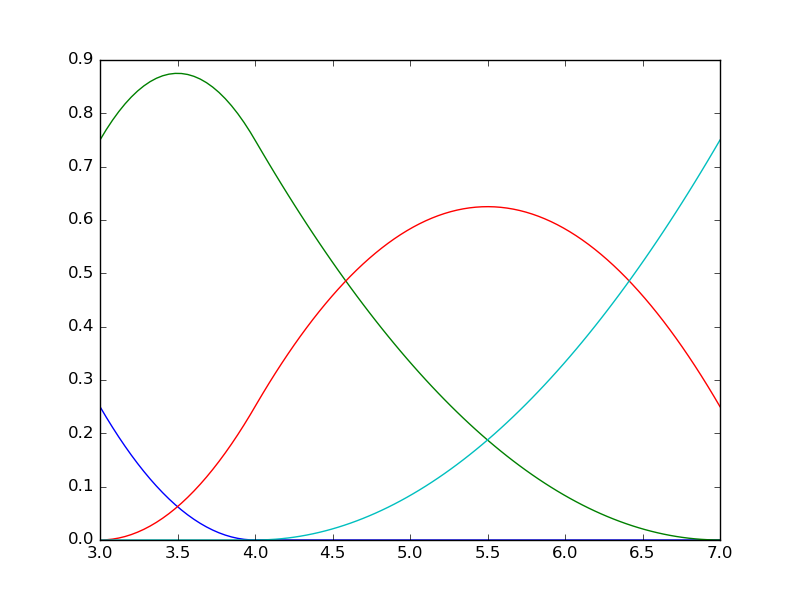
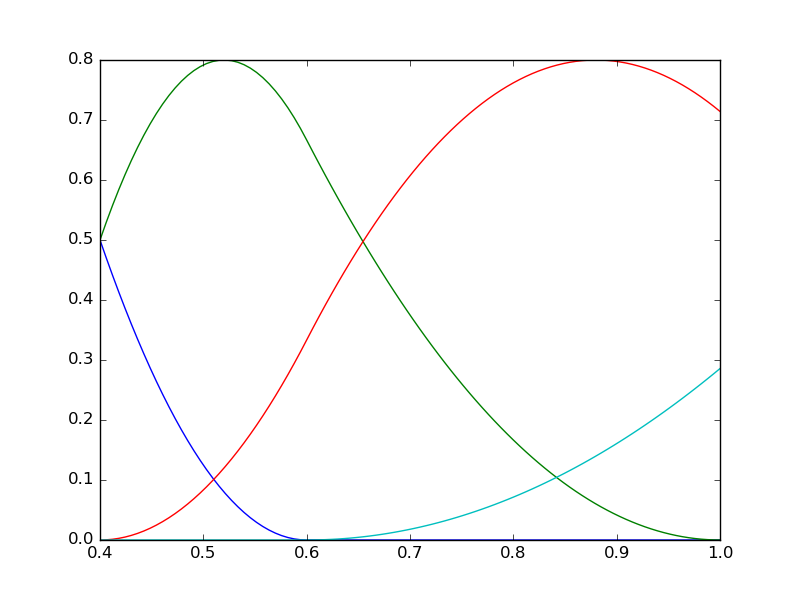
B-Spline curve¶
The B-spline curve in 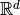 associated to knots vector
associated to knots vector 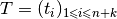 and the control polygon
and the control polygon 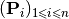 is defined by :
is defined by :
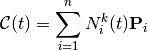
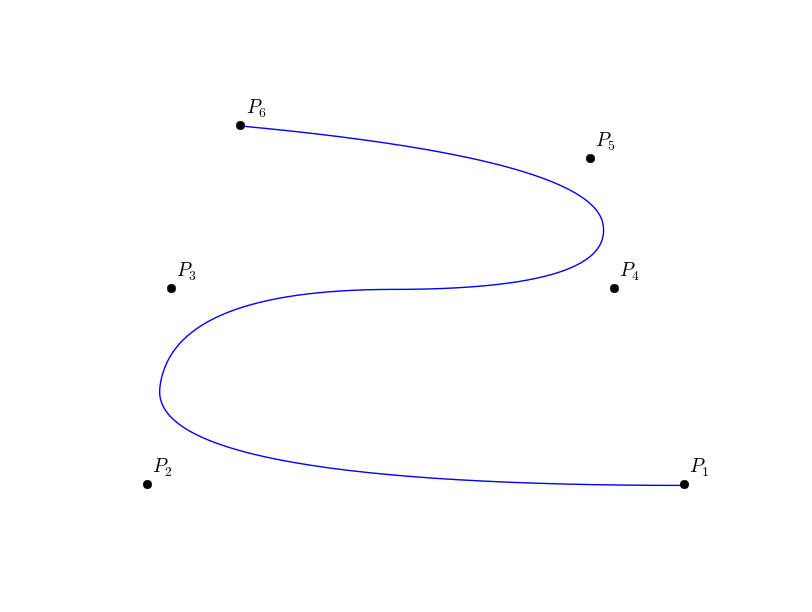
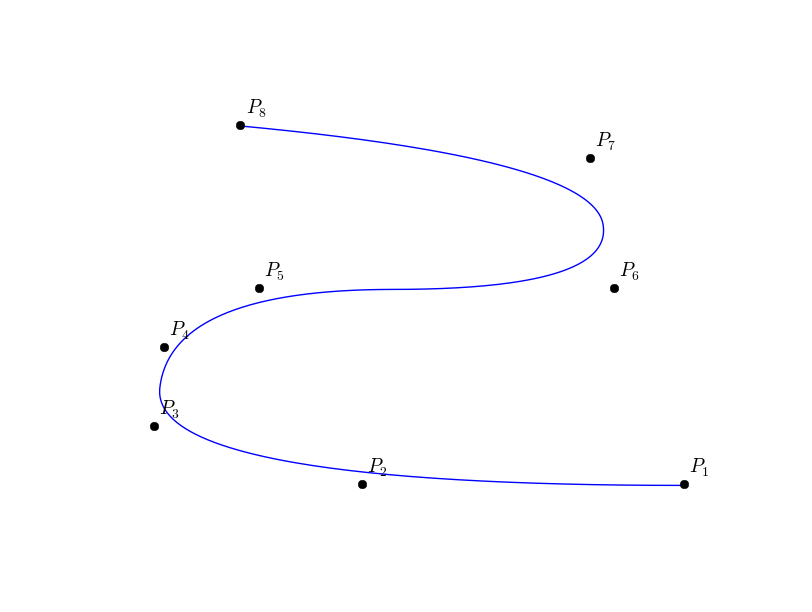
In (Fig. ref{figBSplineCurve}), we give an example of a quadratic B-Spline curve, and its corresponding knot vector and control points.
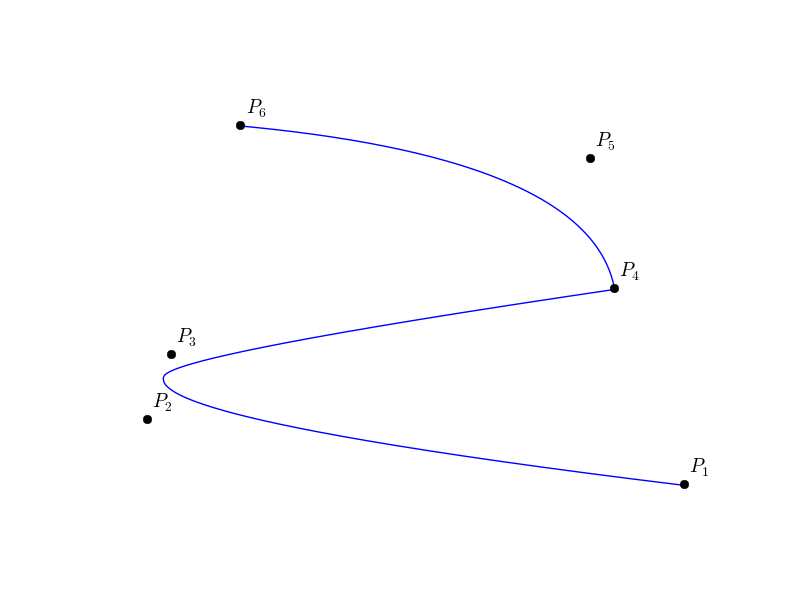
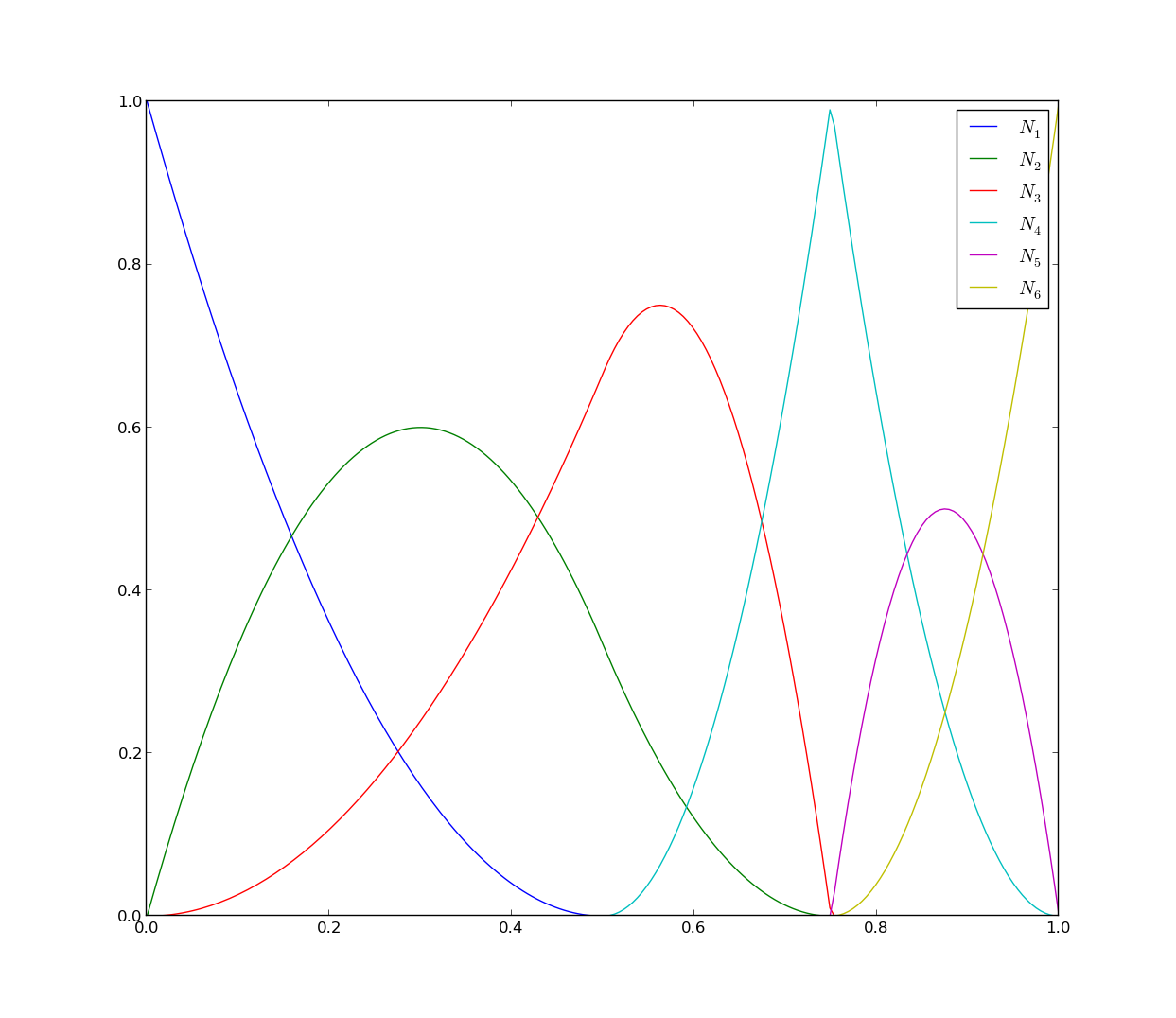
We have the following properties for a B-spline curve:
- If
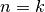 , then
, then  is just a B’ezier-curve,
is just a B’ezier-curve, 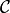 is a piecewise polynomial curve,
is a piecewise polynomial curve,- The curve interpolates its extremas if the associated multiplicity of the first and the last knot are maximum (i.e. equal to
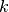 ), i.e. open knot vector,
), i.e. open knot vector, - Invariance with respect to affine transformations,
- Strong convex-hull property:
if 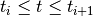 , then
, then 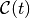 is inside the convex-hull associated to the control points
is inside the convex-hull associated to the control points 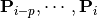 ,
,
- Local modification : moving the
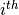 control point
control point 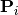 affects
affects 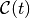 , only in the interval
, only in the interval ![[t_i,t_{i+k}]](../_images/math/0ce0f55484121b1799699bb54757a0781a2914ac.png) ,
, - The control polygon approaches the behavior of the curve.
Note
In order to model a singular curve, we can use multiple control points : 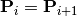 .
.
Multivariate tensor product splines¶
Let us consider 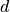 knot vectors
knot vectors 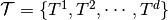 . For simplicity, we consider that these knot vectors are open, which means that
. For simplicity, we consider that these knot vectors are open, which means that 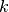 knots on each side are duplicated so that the spline is interpolating on the boundary, and of bounds
knots on each side are duplicated so that the spline is interpolating on the boundary, and of bounds  and
and 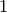 . In the sequel we will use the notation
. In the sequel we will use the notation ![I=[0,1]](../_images/math/1ea1a67b54445a981ff544b1de542bf7525cd491.png) .
Each knot vector
.
Each knot vector 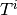 , will generate a basis for a Schoenberg space,
, will generate a basis for a Schoenberg space, 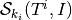 . The tensor product of all these spaces is also a Schoenberg space, namely
. The tensor product of all these spaces is also a Schoenberg space, namely 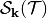 , where
, where 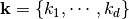 . The cube
. The cube ![\mathcal{P}=I^d=[0,1]^d](../_images/math/3c47cd1746b54679c6db709e271167d2b7907d31.png) , will be referred to as a patch.
, will be referred to as a patch.
The basis for 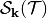 is defined by a tensor product :
is defined by a tensor product :
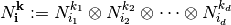
where, 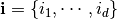 .
.
A typical cell from 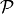 is a cube of the form :
is a cube of the form : ![Q_{\mathbf{i}}=[\xi_{i_1}, \xi_{i_1+1}] \otimes \cdots \otimes [\xi_{i_d}, \xi_{i_d+1}]](../_images/math/83ca350a4ae0007515aecc041132cb71ed522881.png) .
.
Deriving a B-spline curve¶
The derivative of a B-spline curve is obtained as:
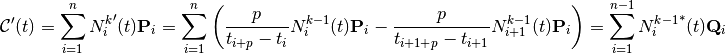
where 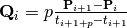 , and
, and 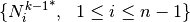 are generated using the knot vector
are generated using the knot vector 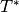 , which is obtained from
, which is obtained from 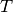 by reducing by one the multiplicity of the first and the last knot (in the case of open knot vector), i.e. by removing the first and the last knot.
by reducing by one the multiplicity of the first and the last knot (in the case of open knot vector), i.e. by removing the first and the last knot.
More generally, by introducing the B-splines family 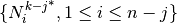 generated by the knots vector
generated by the knots vector 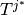 obtained from
obtained from 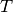 by removing the first and the last knot
by removing the first and the last knot 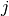 times, we have the following result:
times, we have the following result:
proposition¶
The 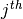 derivative of the curve
derivative of the curve 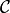 is given by
is given by
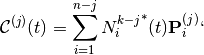
where, for 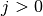
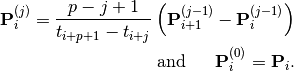
By denoting 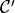 and
and 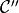 the first and second derivative of the B-spline curve
the first and second derivative of the B-spline curve 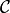 , it is easy to show that:
, it is easy to show that:
We have,
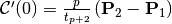 ,
,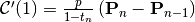 ,
,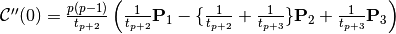 ,
,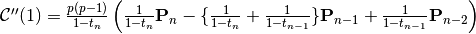 .
.
Example¶
Let us consider the quadratic B-spline curve associated to the knots vector 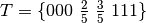 and the control points
and the control points 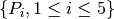 :
:
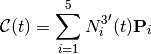
we have,
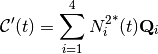
where
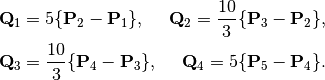
The B-splines 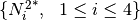 are associated to the knot vector
are associated to the knot vector 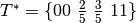 .
.
Fundamental geometric operations
By inserting new knots into the knot vector, we add new control points without changing the shape of the B-Spline curve. This can be done using the DeBoor algorithm [dB01]. We can also elevate the degree of the B-Spline family and keep unchanged the curve [HHM05]. In (Fig. ref{refinement_curve_B_Spline}), we apply these algorithms on a quadratic B-Spline curve and we show the position of the new control points.
Knot insertion¶
After modification, we denote by 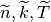 the new parameters.
the new parameters. 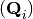 are the new control points.
are the new control points.
One can insert a new knot 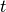 , where
, where 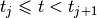 . For this purpose we use the DeBoor algorithm [dB01]:
. For this purpose we use the DeBoor algorithm [dB01]:
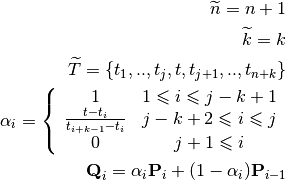
Many other algorithms exist, like blossoming for fast insertion algorithm. For more details about this topic, we refer to [NT93].
Order elevation¶
We can elevate the order of the basis, without changing the curve. Several algorithms exist for this purpose. We used the one by Huang et al. [PP91], [HHM05].
A quadratic B-spline curve and its control points. The knot vector is 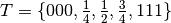 .
.
The curve after a h-refinement by inserting the knots 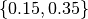 while the degree is kept equal to
while the degree is kept equal to 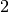 .
.
The curve after a p-refinement, the degree was raised by 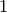 (using cubic B-splines).
(using cubic B-splines).
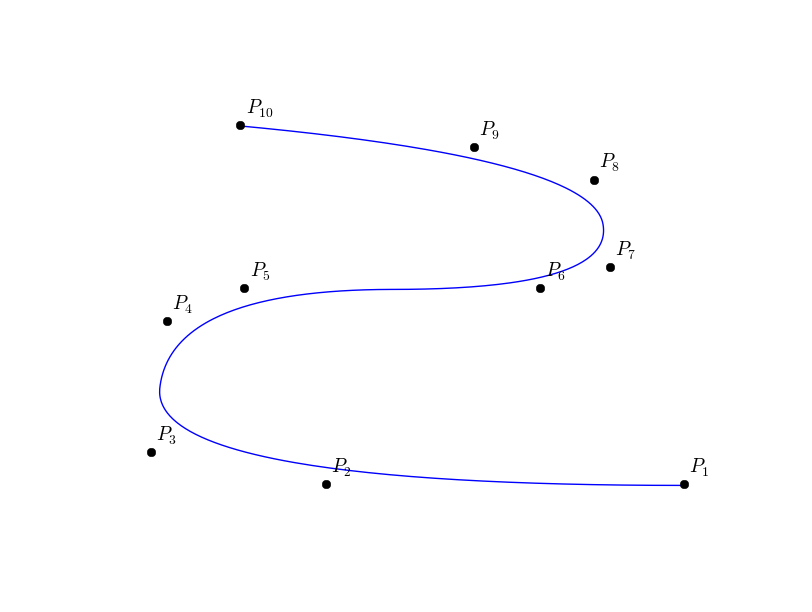
The curve after duplicating the multiplicity of the internal knots 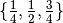 ,
this leads to a B’ezier description. We can then, split the curve into
,
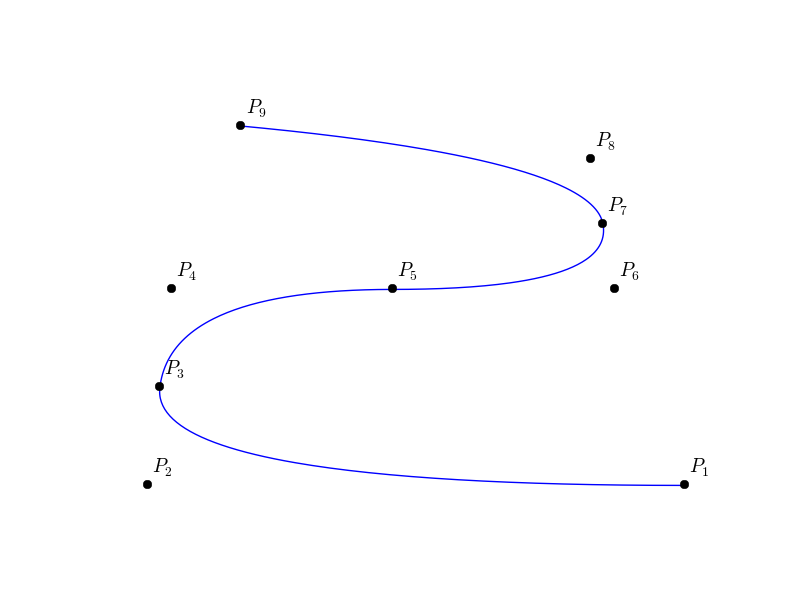
this leads to a B’ezier description. We can then, split the curve into 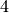 pieces (sub-domains), each one will corresponds to a quadratic B’ezier curve.
pieces (sub-domains), each one will corresponds to a quadratic B’ezier curve.
Translation¶
Rotation¶
Todo
not yet available
Scaling¶
Todo
not yet available
References
| [dB01] | (1, 2) C. de Boor. A Practical Guide to Splines. Applied Mathematical Sciences. Springer New York, 2001. ISBN 9780387953663. URL: https://books.google.de/books?id=m0QDJvBI_ecC. |
| [Far02] | G. Farin. Curves and surfaces for CAGD: a practical guide. Morgan Kaufmann Pub. Inc., San Francisco, CA, USA, 2002. ISBN 1-55860-737-4. |
| [HHM05] | (1, 2) Qi-Xing Huang, Shi-Min Hu, and Ralph R. Martin. Fast degree elevation and knot insertion for b-spline curves. Computer Aided Geometric Design, 22(2):183 – 197, 2005. URL: http://www.sciencedirect.com/science/article/B6TYN-4DXBTHR-2/2/d5b3eec2f4c230c8051623c1c000beae, doi:DOI: 10.1016/j.cagd.2004.11.001. |
| [LP95] | W. Tiller L. Piegl. The NURBS Book. Springer-Verlag, Berlin, Heidelberg, 1995. second ed. |
| [NT93] | Goldman R. N. and Lyche T. Knot Insertion and Deletion Algorithms for B-Spline Curves and Surfaces. SIAM, Philadelphia, USA, 1993. ISBN 9780898713060. |
| [PP91] | Hartmut Prautzsch and Bruce Piper. A fast algorithm to raise the degree of spline curves. Comput. Aided Geom. Des., 8:253–265, October 1991. URL: http://portal.acm.org/citation.cfm?id=124930.124932, doi:10.1016/0167-8396(91)90015-4. |